数学が不得意な子のできない原因のひとつとして、基本となるものが頭の中に入っていないことが挙げられます。 簡単な話、円の面積を求める問題を解くにあたり、円の面積を求める公式が頭になければ正解を出すことはできません。 当たり前のことです。
こがねい数学塾では、数学の基本定理（基本知識）と代表的な問題の解法に関しては、カードで徹底的に反復し、記憶させます。
英単語などを書いたカードを使って反復された方もいるかもしれませんが、それと同じ感覚で、 何度も何度も反復することで頭に叩き込みます。カードに関しては、思考力を養うという目的ではなく、 問題を解くうえで必要な知識を「覚える」ということが目的となります。
カードの知識を利用した実践例
ここでいかに基本知識が重要かを実践例を通してみてみましょう。 以下に、実際の公立高校の入試問題で出題された図形の問題を例題として載せました。
【例題】図形の基本
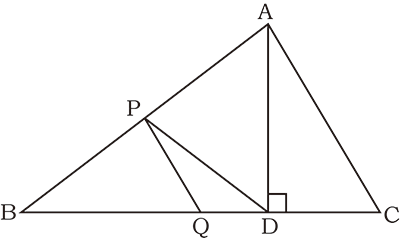上の図において、∠ABC＝33°，∠ACB＝67°，AP＝BP，PQ//AC，AD⊥BCのとき、∠DPQの大きさを求めなさい。
この問題は、簡単そうに見えますが、ある重要なことに気がつかない限り解けません。
その『重要なこと』を入試の試験時間の中で、時間をかけて見つけているようでは、入試は戦えません。
こがねい数学塾の「カード」はこうです。
カードの表面（問題）
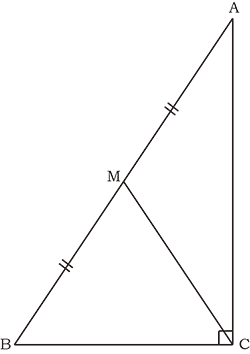直角三角形の斜辺の中点と、直角のある頂点を結んだ線分があるとき、
“即座に反応すべきこと”は何か？
カードの裏面（解答）
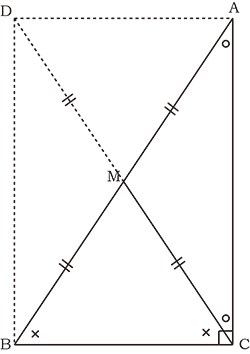“即座に反応すべきこと”は、
AM＝BMにプラスして、CMも等しいこと。
聞けば当たり前に思えるのだが、気が付かないことが多い！！
左図のように長方形を作る補助線を入れれば一目瞭然。
AM＝BM＝CMだから、△MACも△MBCも二等辺三角形といえる。 また、点A、B、Cは、点Mを中心とした円周上にある点ともいえる。
“即座に反応すべきこと”は何か？をカード化し、反復させる。 学校の教科書傍用の問題集にはまずないでしょうし、市販の問題集も、これを単独で強調する問題はないかと思います。
しかし、この問題を解くにあたり、上記のカードが求める「反応」ができれば、 いとも簡単に解くことができるのです。
解答
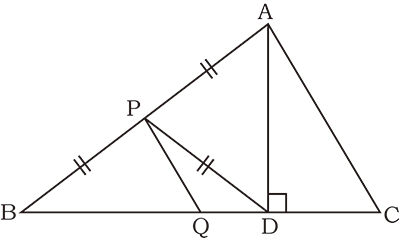
AP＝BP＝PDだから、△PBDと△PADは二等辺三角形といえる。 二等辺三角形の底角は等しいので、 ∠PBD＝∠PDB＝33°
また、PQ//ACより平行線の同位角は等しいので、∠ACB＝∠PQB＝67°
∠PQB＝67°は、△PQDの外角である。すでに、∠PDB＝33°と分かっているので、 求めたい∠DPQは、67－33＝34（度） ・・・（答）
